1026. Maximum Difference Between Node and Ancestor

QUESTION:

Given the root of a binary tree, find the maximum value v for which there exist different nodes a and b where v = |a.val - b.val| and a is an ancestor of b.

A node a is an ancestor of b if either: any child of a is equal to b or any child of a is an ancestor of b.

Example 1: 

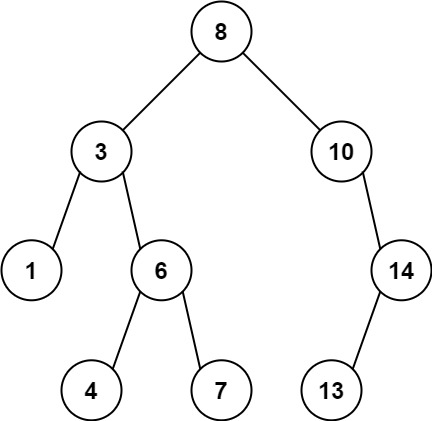
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Example 2: 

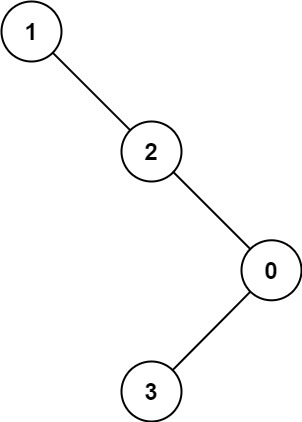
Input: root = [1,null,2,null,0,3]
Output: 3

Constraints:

The number of nodes in the tree is in the range [2, 5000].
0 <= Node.val <= 105

EXPLANATION:

用一个数组去记录, 当前节点的最大值和最小值, 同时记录下结果. 首先看到就肯定能联想到是后序遍历, 那后序遍历之后需要知道左子树的最大最小值和右子树的最大最小值. 这样才能算出最终的结果, 同时需要将自己作为子树, 计算出对应的最大最小值传递就行.

SOLUTION:

class Solution {
    func maxAncestorDiff(_ root: TreeNode?) -> Int {
        return maxAncestorDiffHelper(root)[2]
    }
    func maxAncestorDiffHelper(_ root: TreeNode?) -> [Int] {
        if root == nil {
            return [Int.max, Int.min, -1]
        }
        var left:[Int] = maxAncestorDiffHelper(root?.left)
        var right:[Int] = maxAncestorDiffHelper(root?.right)
        var minVal:Int = min(left[0], right[0], root!.val)
        var maxVal:Int = max(left[1], right[1], root!.val)
        var result:Int = max(abs(root!.val - minVal), abs(root!.val-maxVal))
        return [minVal, maxVal, max(result, left[2], right[2])]
    }
}
>
--> return <--