918. Maximum Sum Circular Subarray

QUESTION:

Given a circular array C of integers represented by A, find the maximum possible sum of a non-empty subarray of C.

Here, a circular array means the end of the array connects to the beginning of the array. (Formally, C[i] = A[i] when 0 <= i < A.length, and C[i+A.length] = C[i] when i >= 0.)

Also, a subarray may only include each element of the fixed buffer A at most once. (Formally, for a subarray C[i], C[i+1], …, C[j], there does not exist i <= k1, k2 <= j with k1 % A.length = k2 % A.length.)

Example 1:

Input: [1,-2,3,-2]
Output: 3
Explanation: Subarray [3] has maximum sum 3

Example 2:

Input: [5,-3,5]
Output: 10
Explanation: Subarray [5,5] has maximum sum 5 + 5 = 10

Example 3:

Input: [3,-1,2,-1]
Output: 4
Explanation: Subarray [2,-1,3] has maximum sum 2 + (-1) + 3 = 4

Example 4:

Input: [3,-2,2,-3]
Output: 3
Explanation: Subarray [3] and [3,-2,2] both have maximum sum 3

Example 5:

Input: [-2,-3,-1]
Output: -1
Explanation: Subarray [-1] has maximum sum -1

Note:

-30000 <= A[i] <= 30000
1 <= A.length <= 30000

EXPLANATION:

首先肯定会想到kadane算法，但是我们同时还需要考虑循环序列的问题，其实我们可以把循环序列展开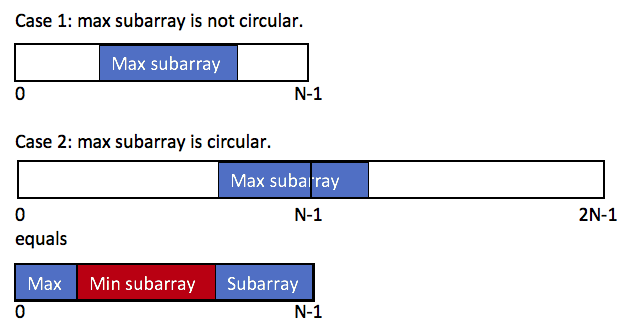， img 第一种情况就是直接使用kadane算法就行，第二种情况我们可以考虑：
最大值 = total - 最小值
这样，我们也可以使用kadane算法来求出最小序列。通过对比两种情况来确定最终的结果。

SOLUTION:

class Solution {
    public int maxSubarraySumCircular(int[] A) {
        int total = 0, maxSum = -30000, curMax = 0, minSum = 30000, curMin = 0;
        for (int a : A) {
            curMax = Math.max(curMax + a, a);
            maxSum = Math.max(maxSum, curMax);
            curMin = Math.min(curMin + a, a);
            minSum = Math.min(minSum, curMin);
            total += a;
        }
        return maxSum > 0 ? Math.max(maxSum, total - minSum) : maxSum;
    }
}
>
--> return <--