1035. Uncrossed Lines

QUESTION:

We write the integers of A and B (in the order they are given) on two separate horizontal lines.

Now, we may draw connecting lines: a straight line connecting two numbers A[i] and B[j] such that:

  1. A[i] == B[j];
  2. The line we draw does not intersect any other connecting (non-horizontal) line. Note that a connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line.

Return the maximum number of connecting lines we can draw in this way.

Example 1: 

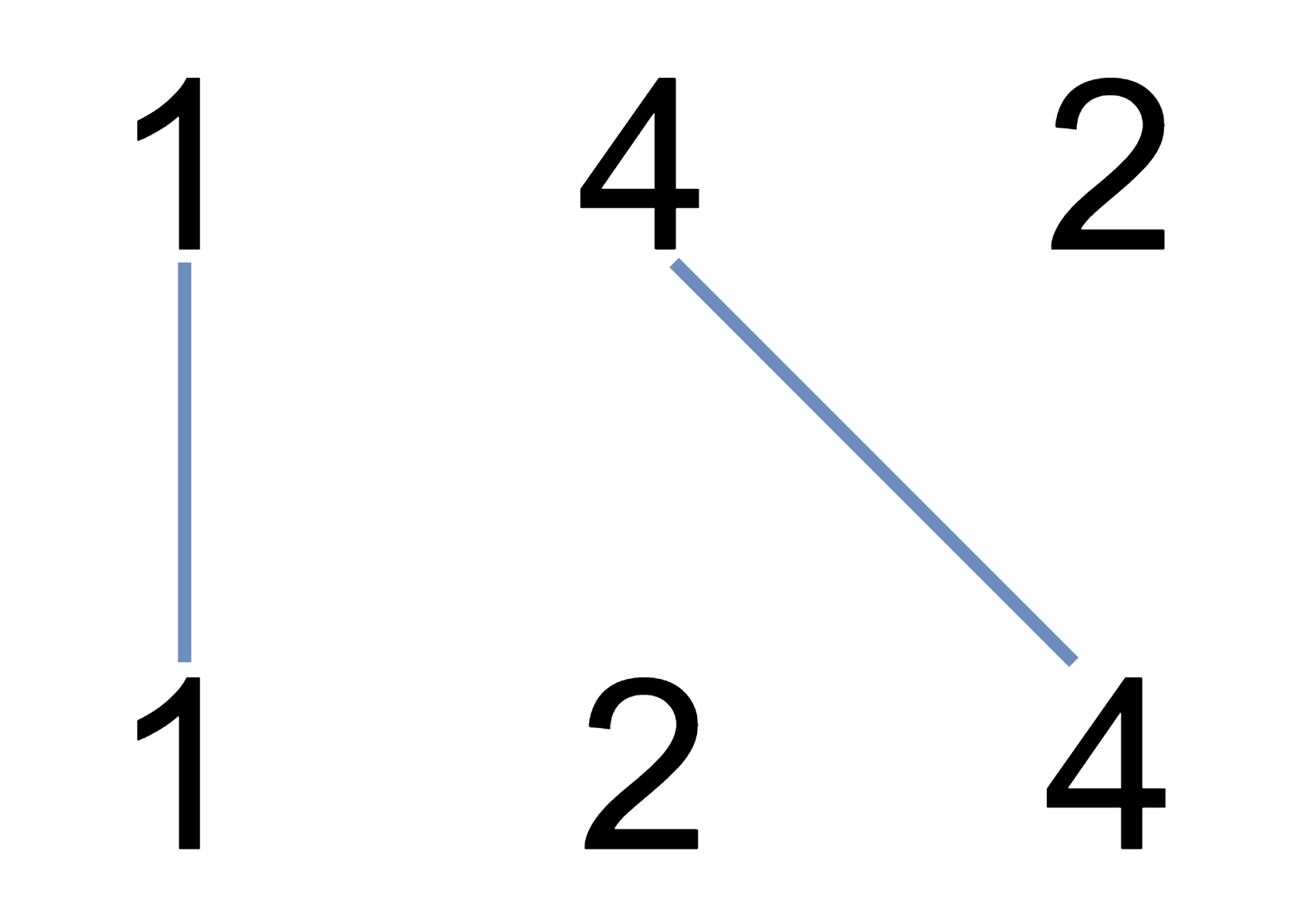
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

Example 2:

Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3

Example 3:

Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2

Note:

1 <= A.length <= 500
1 <= B.length <= 500
1 <= A[i], B[i] <= 2000

EXPLANATION:

看到题意，一开始想到的就是：采用for循环暴力求解，但是很明显，得到了TLE，所以肯定是需要进行优化的，因为暴力求解的方式，时间复杂度就是O(N^2).
那么此时就会想到lcs算法，采用动态规划的方式进行求解。
最后一个数A[i]和B[j]的值如果相等，那么他们的结果就等于dp[i-1][j-1]+1,因为两者可以连在一起。但是如果两者不相等，那么就只能查看Math.max(dp[i-1][j],dp[i][j-1])的两者的大值，于是我们就已经将迭代公式推导了出来。
而第一位数我们是可以确定的，也就是0，那么就可以通过一步一步的方式来获取到最后的答案。

SOLUTION:

    public static int maxUncrossedLines(int[] A, int[] B) {
        int m = A.length, n = B.length, dp[][] = new int[m + 1][n + 1];
        for (int i = 1; i <= m; ++i)
            for (int j = 1; j <= n; ++j)
                if (A[i - 1] == B[j - 1])
                    dp[i][j] = 1 + dp[i - 1][j - 1];
                else
                    dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
        return dp[m][n];
    }
>
--> return <--