1222. Queens That Can Attack the King

QUESTION:

On an 8x8 chessboard, there can be multiple Black Queens and one White King.

Given an array of integer coordinates queens that represents the positions of the Black Queens, and a pair of coordinates king that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King.

Example 1:

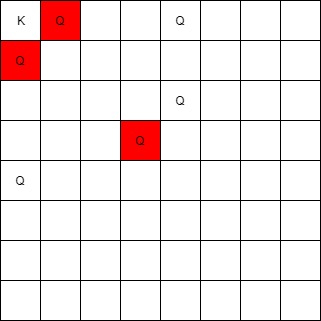
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0] Output: [[0,1],[1,0],[3,3]] Explanation:
The queen at [0,1] can attack the king cause they’re in the same row. The queen at [1,0] can attack the king cause they’re in the same column. The queen at [3,3] can attack the king cause they’re in the same diagnal. The queen at [0,4] can’t attack the king cause it’s blocked by the queen at [0,1]. The queen at [4,0] can’t attack the king cause it’s blocked by the queen at [1,0]. The queen at [2,4] can’t attack the king cause it’s not in the same row/column/diagnal as the king. Example 2:

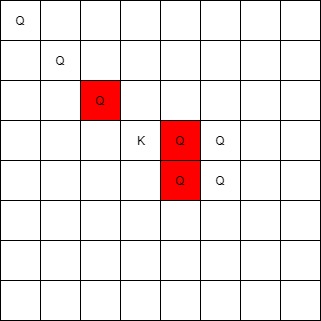
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3] Output: [[2,2],[3,4],[4,4]] Example 3:

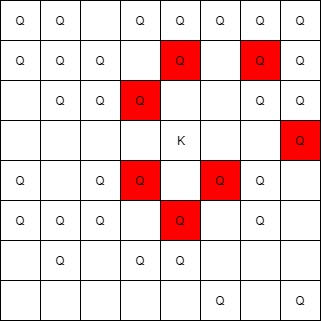
Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4] Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

Constraints:

1 <= queens.length <= 63 queens[0].length == 2 0 <= queens[i][j] < 8 king.length == 2 0 <= king[0], king[1] < 8 At most one piece is allowed in a cell.

EXPLANATION:

做个题目首先还得了解国际象棋，不过从例子中可以看到，queue可以8个方向进行移动，也就是kill，但是queue不能跨越其他单位进行kill。那么我们就可以反向来思考，将king进行8个方向的移动，如果碰到了queue，就说明是可以被kill的，同时，遇到了之后就停止继续那个方向。既然我们需要在棋盘上进行移动，就需要首先将棋盘摆出来。
思路：

  1. 定义一个二维数组用来表示棋盘
  2. 将queue摆放在棋盘上，也就是将棋盘上queue的位置标注为1
  3. 定义8个方向，dx和dy表示每个方向上x，y的delta值
  4. 在每个方向上对king在棋盘范围内进行移动，如果遇到了queue（plant格子==1），那么将该格子放入到结果中，同时终止该方向上的移动
  5. 8个方向都移动结束后返回结果

    SOLUTION:

    class Solution {
 public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) {
     ArrayList<List<Integer>> result = new ArrayList<>();
     int[][] plant = new int[8][8];
     for(int i = 0;i<queens.length;i++){
         plant[queens[i][0]][queens[i][1]] = 1; // 在棋盘上标注queue的位置
     }
     int[] dy = new int[]{0,0,-1,1,-1,1,-1,1};
     int[] dx = new int[]{-1,1,0,0,-1,-1,1,1};// 定义8个方向上的x，y的delta值
     for(int i = 0;i<dy.length;i++) { // 8个方向进行移动
         int x = king[0]+dx[i];
         int y = king[1]+dy[i];
         while (x>=0 && x<=7 && y>=0 && y<=7){ // 移动也就是一直加上对应的dx和dy
             if(plant[x][y]==1){
                 ArrayList<Integer> tmp = new ArrayList<>();
                 tmp.add(x);
                 tmp.add(y);
                 result.add(tmp);
                 break; // 无法跨越其他棋子进行kill，所以在此处进行break，停止该方向上的搜索
             }
             x+=dx[i];
             y+=dy[i];
         }
     }
     return result;
 }
}
>
--> return <--