QUESTION:

Given a 2D grid of size n * m and an integer k. You need to shift the grid k times.

In one shift operation:

Element at grid[i][j] becomes at grid[i][j + 1]. Element at grid[i][m - 1] becomes at grid[i + 1][0]. Element at grid[n - 1][m - 1] becomes at grid[0][0]. Return the 2D grid after applying shift operation k times.

Example 1:

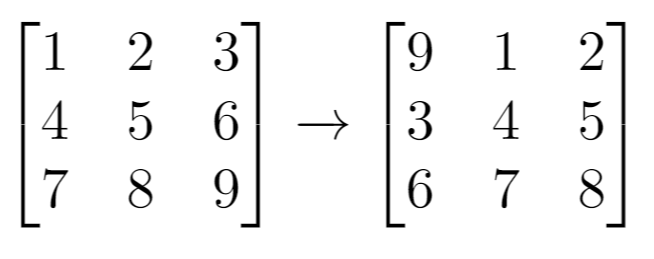
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1 Output: [[9,1,2],[3,4,5],[6,7,8]] Example 2:

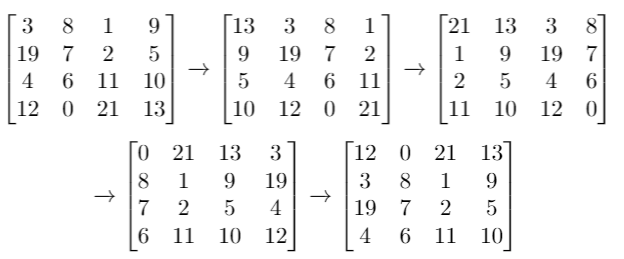Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4 Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]] Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9 Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints:

1 <= grid.length <= 50 1 <= grid[i].length <= 50 -1000 <= grid[i][j] <= 1000 0 <= k <= 100

EXPLANATION:

看到题目后，再审一下，发现需要返回的是一个list，那么就说明是可以改变数据结构的。首先想到的就是首尾相连的linkedlist，通过移动k位后，再重新进行填充。就依照这个思路。
逻辑：
1.首先将数组存放在链表中
2.计算开始的位置： index就为往前走k步。
|————–|————————-|
k 0 nm
这样就很清楚了，那么k的位置其实就是nm-k的位置，然后向后开始计算就行。同时需要考虑k>nm的情况
3.按照index位置，作为0开始添加，当k>nm的时候就预设为0重新添加 4.将添加的结果添加到集合中

SOLUTION:

class Solution {
    public List<List<Integer>> shiftGrid(int[][] grid, int k) {
                LinkedList<Integer> ll = new LinkedList<>();
        for(int i = 0;i<grid.length;i++){
            for(int j = 0;j<grid[i].length;j++){
                ll.add(grid[i][j]);
            }
        }
        List<List<Integer>> result = new ArrayList<>();
        int index = grid.length*grid[0].length-k < 0 ? grid.length*grid[0].length - k%(grid.length*grid[0].length) :grid.length*grid[0].length-k ;
        for(int i = 0;i<grid.length;i++){
            List<Integer> tmp = new ArrayList<>();
            for(int j = 0;j<grid[i].length;j++){
                if(index==grid.length*grid[i].length) index= 0;
                tmp.add(ll.get(index));
                index++;
            }
            result.add(tmp);
        }
        return result;
    }
}