1557. Minimum Number of Vertices to Reach All Nodes

QUESTION:

Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.

Find the smallest set of vertices from which all nodes in the graph are reachable. It’s guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

Example 1: 

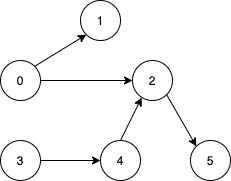
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

Example 2: 

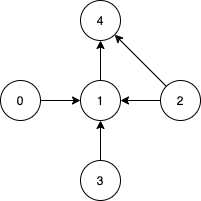
Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

Constraints:

2 <= n <= 10^5
1 <= edges.length <= min(10^5, n * (n - 1) / 2)
edges[i].length == 2
0 <= fromi, toi < n
All pairs (fromi, toi) are distinct.

EXPLANATION:

题目虽然是medium的, 但是还是挺简单的. 只需要确定没有指向自己的点, 那么这个点就是一个孤立的点. 把这些孤立的点集合就是需要的结果.用一个boolean的数组来标记. index表示点的值. bool[index]表示是否有指向自己.
1.首先for循环取出edges[i][1],拿到被指向的数
2.把这个被指向的数作为index,在bool array里标记为有指向
3.遍历bool array, 将没有被指向的index放到结果中

SOLUTION:

class Solution {
    func findSmallestSetOfVertices(_ n: Int, _ edges: [[Int]]) -> [Int] {
        var arr:[Bool] = Array(repeating: false, count: n)
        var result:[Int] = []
        for edge in edges {
            arr[edge[1]] = true
        }
        for index in arr.indices {
            if (!arr[index]) {
                result.append(index)
            }
        }
        return result
    }
}
>
--> return <--