1582. Special Positions in a Binary Matrix

QUESTION:

Given an m x n binary matrix mat, return the number of special positions in mat.

A position (i, j) is called special if mat[i][j] == 1 and all other elements in row i and column j are 0 (rows and columns are 0-indexed).

Example 1: 

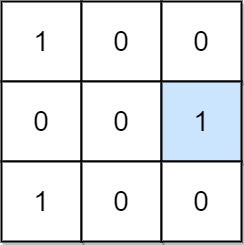
Input: mat = [[1,0,0],[0,0,1],[1,0,0]]
Output: 1
Explanation: (1, 2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.

Example 2: 

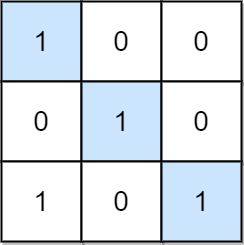
Input: mat = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3
Explanation: (0, 0), (1, 1) and (2, 2) are special positions.

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 100
mat[i][j] is either 0 or 1.

EXPLANATION:

for循环遍历每一个数, 如果是1, 就拿出来看看改行该列是不是只有这一个. 是的话就结果+1

SOLUTION:

class Solution {
    func numSpecial(_ mat: [[Int]]) -> Int {
        var result:Int = 0
        for indexI in mat.indices {
            for indexJ in mat[indexI].indices {
                if mat[indexI][indexJ] == 1 {
                    if numSpecialHelper(mat, indexI: indexI, IndexJ: indexJ) {
                        result += 1
                    }
                }
            }
        }
        return result
    }
    
    func numSpecialHelper(_ mat: [[Int]], indexI:Int , IndexJ:Int) -> Bool {
        var result:Bool = true
        var sum:Int = 0
        for num in mat[indexI] {
            sum += num
        }
        if sum != 1 {
            return false
        }
        sum = 0
        for indexC in 0...mat.count - 1 {
            sum += mat[indexC][IndexJ]
        }
        if sum != 1 {
            return false
        }
        return result
    }
}
>
--> return <--