1637. Widest Vertical Area Between Two Points Containing No Points

QUESTION:

Given n points on a 2D plane where points[i] = [xi, yi], Return the widest vertical area between two points such that no points are inside the area.

A vertical area is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The widest vertical area is the one with the maximum width.

Note that points on the edge of a vertical area are not considered included in the area.

Example 1: 

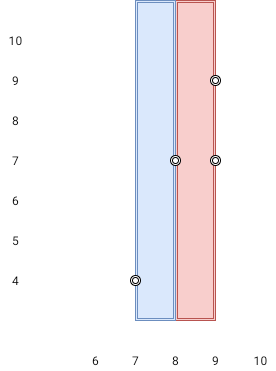
Input: points = [[8,7],[9,9],[7,4],[9,7]]
Output: 1
Explanation: Both the red and the blue area are optimal.

Example 2:

Input: points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
Output: 3

Constraints:

n == points.length
2 <= n <= 105
points[i].length == 2
0 <= xi, yi <= 109

EXPLANATION:

这题就很简单了, 主要其实就是为了比较每个点的x的值,只要两个x值最大,那么就说明他们中间的距离是最大的
思路:

  1. 对points进行排序, 依据就是x的值
  2. 对排序后的点进行计算, 获取到相邻两个点x差的最大值

SOLUTION:

class Solution {
    fun maxWidthOfVerticalArea(points: Array<IntArray>): Int {
        Arrays.sort(points, kotlin.Comparator { o1, o2 -> o1[0]-o2[0] })
        var result : Int = 0
        for (tmp in 1 until points.size)
            result = Math.max(result,points[tmp][0] - points[tmp-1][0])
        return result
    }
}
--> return <--