1971. Find if Path Exists in Graph

QUESTION:

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex source to vertex destination.

Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.

Example 1: 

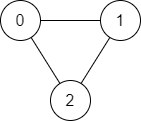
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

Example 2: 

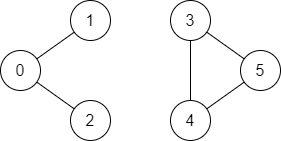
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.

Constraints:

1 <= n <= 2 * 105
0 <= edges.length <= 2 * 105
edges[i].length == 2
0 <= ui, vi <= n - 1
ui != vi
0 <= source, destination <= n - 1
There are no duplicate edges.
There are no self edges.

EXPLANATION:

采用dfs的方法, 用一个visted来记录已经已经走过的, 来预防形成环状的情况. 我们首先将所有点可以到达的点都记录下来. 然后用一个queue去从头开始搜索. 搜索所有的路径 , 如果路径中有destination,就说明找到了, 否则就说明没有找到了.

SOLUTION:

class Solution {
    func validPath(_ n: Int, _ edges: [[Int]], _ source: Int, _ destination: Int) -> Bool {
        var graph = [[Int]](repeating: [], count: n)
        
        for edge in edges {
            graph[edge[0]].append(edge[1])
            graph[edge[1]].append(edge[0])
        }
        
        var arr: [Int] = [source]
        var visited = Set<Int>()
        while !arr.isEmpty {
            var tmp = arr.removeFirst()
            visited.insert(tmp)
            if (tmp == destination) {
                return true
            }
            
            for edge in graph[tmp] {
                if !visited.contains(edge) {
                    arr.append(edge)
                }
            }
        }
        return false
    }
}
--> return <--