QUESTION:
There is an n x n grid, with the top-left cell at (0, 0) and the bottom-right cell at (n - 1, n - 1). You are given the integer n and an integer array startPos where startPos = [startrow, startcol] indicates that a robot is initially at cell (startrow, startcol).
You are also given a 0-indexed string s of length m where s[i] is the ith instruction for the robot: ‘L’ (move left), ‘R’ (move right), ‘U’ (move up), and ‘D’ (move down).
The robot can begin executing from any ith instruction in s. It executes the instructions one by one towards the end of s but it stops if either of these conditions is met:
The next instruction will move the robot off the grid. There are no more instructions left to execute. Return an array answer of length m where answer[i] is the number of instructions the robot can execute if the robot begins executing from the ith instruction in s.
Example 1:
Input: n = 3, startPos = [0,1], s = "RRDDLU"
Output: [1,5,4,3,1,0]
Explanation: Starting from startPos and beginning execution from the ith instruction:
- 0th: "RRDDLU". Only one instruction "R" can be executed before it moves off the grid.
- 1st: "RDDLU". All five instructions can be executed while it stays in the grid and ends at (1, 1).
- 2nd: "DDLU". All four instructions can be executed while it stays in the grid and ends at (1, 0).
- 3rd: "DLU". All three instructions can be executed while it stays in the grid and ends at (0, 0).
- 4th: "LU". Only one instruction "L" can be executed before it moves off the grid.
- 5th: "U". If moving up, it would move off the grid.
Example 2:
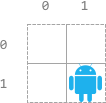
Input: n = 2, startPos = [1,1], s = "LURD"
Output: [4,1,0,0]
Explanation:
- 0th: "LURD".
- 1st: "URD".
- 2nd: "RD".
- 3rd: "D".
Example 3:
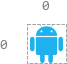
Input: n = 1, startPos = [0,0], s = "LRUD"
Output: [0,0,0,0]
Explanation: No matter which instruction the robot begins execution from, it would move off the grid.
Constraints:
m == s.length
1 <= n, m <= 500
startPos.length == 2
0 <= startrow, startcol < n
s consists of 'L', 'R', 'U', and 'D'.
EXPLANATION:
这虽然是一道medium的题目, 但是逻辑还是比较简单的. 因为我们需要对每一步的操作进行上下左右移动. 那么就是对x,y进行修改, 那么我们只要做出对应的映射表就可以.
1.做出对应的映射表, 上下左右,分别的x,y操作写上
2.遍历s, 从第一位开始
3.获取到上下左右移动,对对应的xy进行操作
4.判断移动后位置在不在grid里
5.循环到最后一位, 将结果添加到result中
6.重复2-5步
SOLUTION:
class Solution {
func executeInstructions(_ n: Int, _ startPos: [Int], _ s: String) -> [Int] {
var charArray:[Character] = ["U","D","L","R"]
var operationX:[Int] = [-1,1,0,0]
var operationY:[Int] = [0,0,-1,1]
var result:[Int] = []
var sArray = Array(s)
for i in 0...sArray.count-1 {
var tmpResult = 0;
var tmpStartPos:[Int] = [startPos[0], startPos[1]]
for j in i...sArray.count-1 {
var index = charArray.index(of: sArray[j])
tmpStartPos[0] = tmpStartPos[0] + operationX[index!]
tmpStartPos[1] = tmpStartPos[1] + operationY[index!]
if (tmpStartPos[0] >= 0 && tmpStartPos[0] <= n-1
&& tmpStartPos[1] >= 0 && tmpStartPos[1] <= n-1) {
tmpResult+=1
} else {
break
}
}
result.append(tmpResult)
}
return result
}
}