QUESTION:
You are given two integers m and n, which represent the dimensions of a matrix.
You are also given the head of a linked list of integers.
Generate an m x n matrix that contains the integers in the linked list presented in spiral order (clockwise), starting from the top-left of the matrix. If there are remaining empty spaces, fill them with -1.
Return the generated matrix.
Example 1:
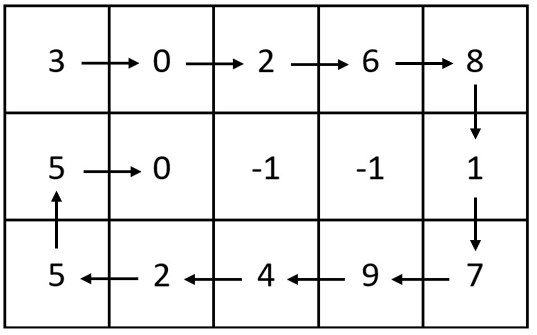
Input: m = 3, n = 5, head = [3,0,2,6,8,1,7,9,4,2,5,5,0]
Output: [[3,0,2,6,8],[5,0,-1,-1,1],[5,2,4,9,7]]
Explanation: The diagram above shows how the values are printed in the matrix.
Note that the remaining spaces in the matrix are filled with -1.
Example 2:
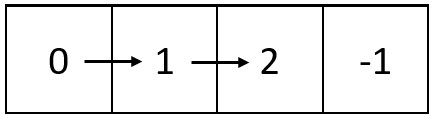
Input: m = 1, n = 4, head = [0,1,2]
Output: [[0,1,2,-1]]
Explanation: The diagram above shows how the values are printed from left to right in the matrix.
The last space in the matrix is set to -1.
Constraints:
1 <= m, n <= 105
1 <= m * n <= 105
The number of nodes in the list is in the range [1, m * n].
0 <= Node.val <= 1000
EXPLANATION:
这是一道medium的题目, 主要是坐标的操作, 坐标需要不停地移动, 那么我们就可以先确定出, 移动的次数一定小于等于head的链表长度, 从限制中得到的. 那么问题就变成了, 怎么去操作坐标, 顺时针就是每次转弯的时候对xy就行操作, 那么我们只要把每次xy操作的值记录下来, 同时用direction去表示当前的方向. 那么什么时候转向呢, 1个就是到了边界, 另外就是已经进行了赋值, 从题目中可以得到, head的值永远都是大于0的. 那么我们就可以用-1来判断是否进行了赋值.
SOLUTION:
class Solution {
func spiralMatrix(_ m: Int, _ n: Int, _ head: ListNode?) -> [[Int]] {
var result: [[Int]] = Array(repeating: Array(repeating: -1, count: n), count: m)
let xChange:[Int] = [0,1,0,-1] // 坐标x的操作
let yChange:[Int] = [1,0,-1,0] // 坐标y的操作
var direction:Int = 0
var pos:[Int] = [0,0]
var head = head
while head != nil {
result[pos[0]][pos[1]] = head!.val
head = head?.next
var posX:Int = pos[0] + xChange[direction % 4]
var posY:Int = pos[1] + yChange[direction % 4]
if posX < 0 || posX >= m || posY < 0 || posY >= n || result[posX][posY] != -1 {
// 超出了范围或者已经赋值
direction += 1
posX = pos[0] + xChange[direction % 4]
posY = pos[1] + yChange[direction % 4]
}
pos = [posX, posY]
}
return result
}
}