2373. Largest Local Values in a Matrix

QUESTION:

You are given an n x n integer matrix grid.

Generate an integer matrix maxLocal of size (n - 2) x (n - 2) such that:

maxLocal[i][j] is equal to the largest value of the 3 x 3 matrix in grid centered around row i + 1 and column j + 1. In other words, we want to find the largest value in every contiguous 3 x 3 matrix in grid.

Return the generated matrix.

Example 1: 

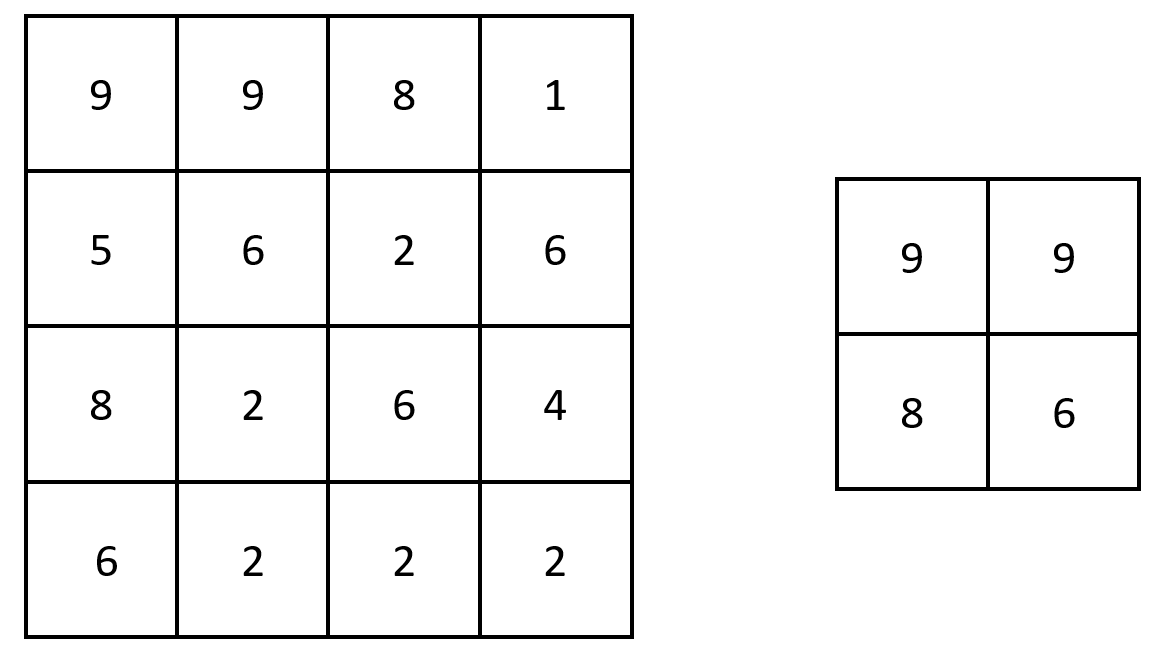
Input: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
Output: [[9,9],[8,6]]
Explanation: The diagram above shows the original matrix and the generated matrix.
Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.

Example 2: 

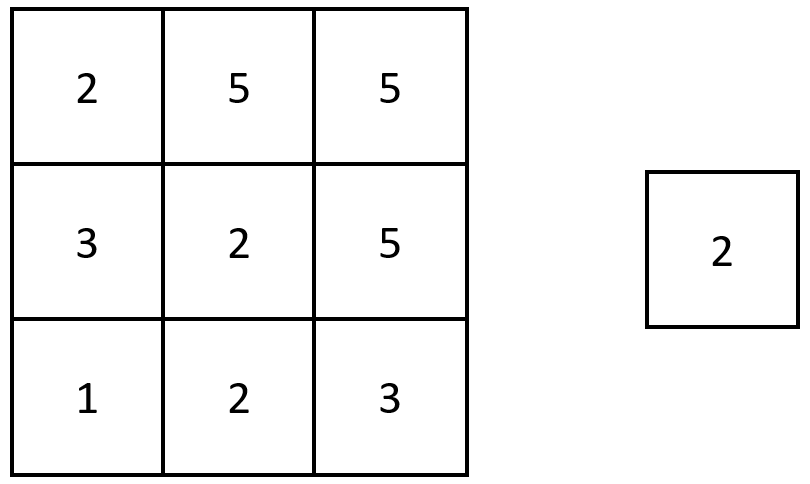
Input: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
Output: [[2,2,2],[2,2,2],[2,2,2]]
Explanation: Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.

Constraints:

n == grid.length == grid[i].length
3 <= n <= 100
1 <= grid[i][j] <= 100

EXPLANATION:

就比较简单了, 也没有什么特别需要注意的点, 就是一个暴力查询的问题.

SOLUTION:

class Solution {
    func largestLocal(_ grid: [[Int]]) -> [[Int]] {
        var result:[[Int]] = []
        for indexI in 1...grid.count - 2 {
            var arr:[Int] = []
            for indexJ in 1...grid[indexI].count - 2 {
                arr.append(largestLocalHelper(grid, indexI, indexJ))
            }
            result.append(arr)
        }
        return result
    }
    
    func largestLocalHelper(_ grid: [[Int]], _ i: Int, _ j: Int) -> Int {
        return max(grid[i][j], grid[i-1][j-1], grid[i+1][j+1], grid[i-1][j],grid[i+1][j],grid[i][j-1],grid[i][j+1],grid[i+1][j-1],grid[i-1][j+1])
    }
}
>
--> return <--