QUESTION:
You are given an m x n integer matrix grid.
We define an hourglass as a part of the matrix with the following form:

Return the maximum sum of the elements of an hourglass.
Note that an hourglass cannot be rotated and must be entirely contained within the matrix.
Example 1:
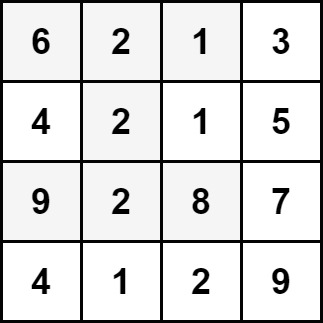
Input: grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]]
Output: 30
Explanation: The cells shown above represent the hourglass with the maximum sum: 6 + 2 + 1 + 2 + 9 + 2 + 8 = 30.
Example 2:
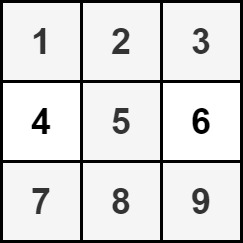
Input: grid = [[1,2,3],[4,5,6],[7,8,9]]
Output: 35
Explanation: There is only one hourglass in the matrix, with the sum: 1 + 2 + 3 + 5 + 7 + 8 + 9 = 35.
Constraints:
m == grid.length
n == grid[i].length
3 <= m, n <= 150
0 <= grid[i][j] <= 106
EXPLANATION:
按照题意要求, 模拟出来即可.
SOLUTION:
class Solution {
func maxSum(_ grid: [[Int]]) -> Int {
var result = 0
for i in 0..<grid.count - 2 {
for j in 0..<grid[i].count - 2 {
var tmp = 0
tmp = grid[i][j] + grid[i][j+1] + grid[i][j+2] + grid[i+1][j+1] + grid[i+2][j] + grid[i+2][j+1] + grid[i+2][j+2]
result = max(result, tmp)
}
}
return result
}
}