812. Largest Triangle Area

QUESTION:

You have a list of points in the plane. Return the area of the largest triangle that can be formed by any 3 of the points.

Example:
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2
Explanation: 
The five points are show in the figure below. The red triangle is the largest.

img

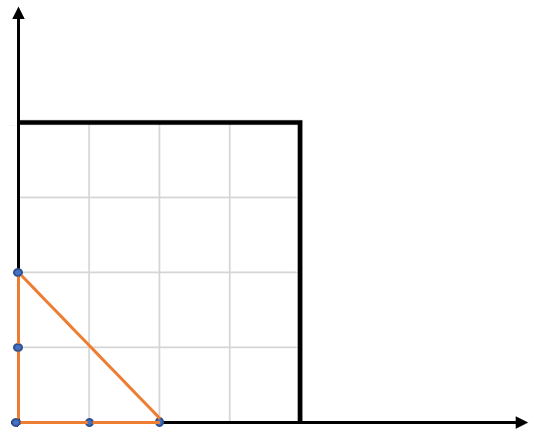
Notes:

  • 3 <= points.length <= 50.
  • No points will be duplicated.
  • -50 <= points[i][j] <= 50.
  • Answers within 10^-6 of the true value will be accepted as correct.

EXPLANATION:

emm这个想了一些办法，后来看起来还是只能采用穷举法。

1.计算出三边的边长

2.通过海伦公式，计算出结果。

SOLUTION:

class Solution {
    public double largestTriangleArea(int[][] points) {
        double result = 0;
        for(int i = 0;i<points.length-2;i++){
            for(int j = i+1;j<points.length-1;j++){
                for(int m = j+1;m<points.length;m++){
                    int[] A = points[i];
                    int[] B = points[j];
                    int[] C = points[m];
                    double disA = dis(A,B);
                    double disB = dis(A,C);
                    double disC = dis(C,B);
                    if(!largestTriangleAreaHelper(disA,disB,disC))continue;
                    double p = (disA+disB+disC)/2;
                    double field = Math.sqrt(p*(p-disA)*(p-disB)*(p-disC));
                    result = Math.max(result,field);
                }
            }
        }
        return result;
    }
    
    public static double dis(int[] A,int[] B){
        double dis = (A[0]-B[0])*(A[0]-B[0])+(A[1]-B[1])*(A[1]-B[1]);
        dis = Math.sqrt(dis);
        return dis;
    }
    public static boolean largestTriangleAreaHelper(double disA,double disB,double disC){
        if(disA<(disB+disC)&&disB<(disA+disC)&&disC<(disA+disB))return true;
        return false;
    }
}
>
--> return <--