QUESTION:
On a 2 dimensional grid with R rows and C columns, we start at (r0, c0) facing east.
Here, the north-west corner of the grid is at the first row and column, and the south-east corner of the grid is at the last row and column.
Now, we walk in a clockwise spiral shape to visit every position in this grid.
Whenever we would move outside the boundary of the grid, we continue our walk outside the grid (but may return to the grid boundary later.)
Eventually, we reach all R * C spaces of the grid.
Return a list of coordinates representing the positions of the grid in the order they were visited.
Example 1:
Input: R = 1, C = 4, r0 = 0, c0 = 0 Output: [[0,0],[0,1],[0,2],[0,3]]
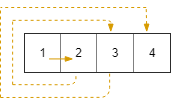
Example 2:
Input: R = 5, C = 6, r0 = 1, c0 = 4 Output: [[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]
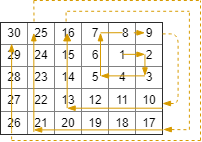
Note:
1 <= R <= 100 1 <= C <= 100 0 <= r0 < R 0 <= c0 < C
EXPLANATION:
首先需要理一下思路。题意很容易理解,按照顺时针方向旋转读取,按照顺序给出结果。那么我的思路就是:
1.首先将所有的顺时针的点都获取到
2.再将不在矩形范围内的点剔除
剔除就比较简单了,只要判断这个点的横纵坐标范围就可以。那么难点就来到了第一个将所有点都获取到。顺时针旋转,没个点都取到,那就是一圈一圈的圆叠加在一起,经过例子,我们可以发现,第一圈是的半径c0+1,r0+1,c0-1,r0-1,而第二圈是c0+2,r0+2,。。。第n圈的半径就是(r0+n,c0+n),那方向我们怎么计算呢。按照以前的思路,可以定义数组的正负来替代方向。而最大的圈数也就是r0,c0离这个矩阵最远的距离。所以思路有了。就开始写代码。
SOLUTION:
class Solution {
public int[][] spiralMatrixIII(int R, int C, int r0, int c0) {
int[] dr = {0,1,0,-1};
int[] dc = {1,0,-1,0};// 定义方向取值
int round = 1;
int maxRround = Math.max(r0+1,R-r0-1); // r0 到 row的最大值
int maxCround = Math.max(c0+1,C-c0-1); // c0 到colum的最大值
int maxRound = Math.max(maxRround,maxCround); // 最大的圈数
int direction = 0; // 定义方向
int[] position = {r0,c0}; // 初始点
List<int[]> result = new ArrayList<>();
while (round<=maxRound){ // 每次跑圈
while (direction<=3){ // 跑完4个方向
switch (direction){
case 0: // 向右
while (position[1]<c0+dc[direction]*round){
int[] tmp = new int[2];
position[0] += dr[direction];
tmp[0] = position[0];
position[1] += dc[direction];
tmp[1] = position[1];
result.add(tmp);
}
break;
case 1: // 向下
while (position[0]<r0+dr[direction]*round){
int[] tmp = new int[2];
position[0] += dr[direction];
tmp[0] = position[0];
position[1] += dc[direction];
tmp[1] = position[1];
result.add(tmp);
}
break;
case 2: // 向左
while (position[1]>c0+dc[direction]*round){
int[] tmp = new int[2];
position[0] += dr[direction];
tmp[0] = position[0];
position[1] += dc[direction];
tmp[1] = position[1];
result.add(tmp);
}
break;
case 3: // 向上
while (position[0]>r0+dr[direction]*round){
int[] tmp = new int[2];
position[0] += dr[direction];
tmp[0] = position[0];
position[1] += dc[direction];
tmp[1] = position[1];
result.add(tmp);
}
break;
}
direction++;
}
direction = 0;
round++;
}
result.add(0,new int[]{r0,c0});//不能忘记把起点放在第一个位置
Iterator<int[]> iterator = result.iterator();
while (iterator.hasNext()){ // 剔除不在矩形范围内的点
int[] next = iterator.next();
if(next[0]<0 || next[0]>=R || next[1]<0 || next[1]>=C) iterator.remove();
}
int[][] rResult = new int[result.size()][2];
for(int i = 0;i<result.size();i++){
rResult[i][0] = result.get(i)[0];
rResult[i][1] = result.get(i)[1];
}
return rResult;
}
}