QUESTION:

A full binary tree is a binary tree where each node has exactly 0 or 2 children.

Return a list of all possible full binary trees with N nodes. Each element of the answer is the root node of one possible tree.

Each node of each tree in the answer must have node.val = 0.

You may return the final list of trees in any order.

Example 1:

Input: 7 Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]] Explanation:

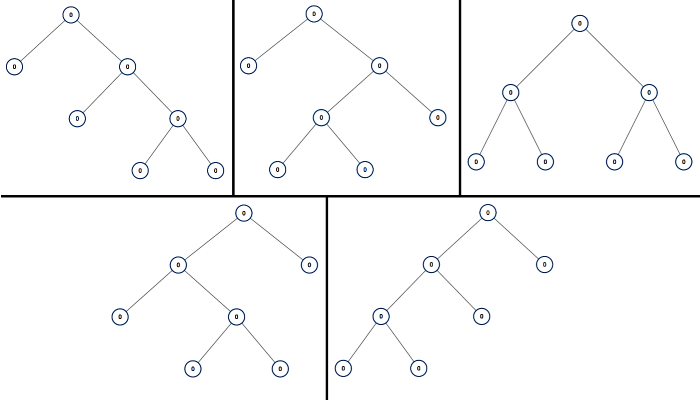
Note:

1 <= N <= 20

EXPLANATION:

首先需要从1往后开始找规律：
1.第一个规律是：偶数肯定不行，因为根节点有一个，其他的节点都是两个，那么就肯定回事奇数。
2.第二个规律是：就是需要两个两个的进行摆放，要不然一个不摆，要不然就是2，于是step就是2.
然后再接着看规律：
N = 1的时候 那么只有一个节点
N = 3 时候，只有一个结果，就是 [0,0,0]
N = 5 时候，有两个结果是[[0,0,0,0,0],[0,0,0,null,null,0,0]] 就是f(5) = f(1+f(3)) + f(f(3)+1) 那么就可以得到规律： 每个数都是 如 7 = (1+f(5)) + (f(5)+1)+ (f(3)+f(3)) 得到一个递归的公式。

SOLUTION:

class Solution {
    public List<TreeNode> allPossibleFBT(int N) {
                if(N % 2 ==0) return new ArrayList<>();
        List<TreeNode> res = new ArrayList<>();
        if(N == 1) {
            res.add(new TreeNode(0));
            return res;
        }
        for(int i = 1; i < N; i += 2) {
            List<TreeNode> leftSubTrees = allPossibleFBT(i);
            List<TreeNode> rightSubTrees = allPossibleFBT(N - i - 1);
            for(TreeNode l : leftSubTrees) {
                for(TreeNode r : rightSubTrees) {
                    TreeNode root = new TreeNode(0);
                    root.left = l;
                    root.right = r;
                    res.add(root);
                }
            }
        }
        return res;
    }
}